第二章数据表示总结与练习
一、总结
真值: 正号和负号分别用“ + ”和“ - ”表示,数据位保持二进制值不变的数据表示方法。
数值数据:计算机所支持的一种数据类型,用于科学计算,常见的数值数据类型包括小数、整数、浮点数数等。
非数值数据:计算机所支持的一种数据类型,一般用来表示符号或文字等没有数值值的数据。
机器数:数据在机器中的表示形式,是正负符号数码化后的二进制数据。
变形补码:用两个二进制位来表示数字的符号位,其余与补码相同。即“ 00 ”表示正,“ 11 ”表示负。
规格化:将非规格化的数处理成规格化数的过程。规格化数规定尾数用纯小数表示,且真值表示时小数点后第一位不为 0 (以机器数表示时对小数点后第一位的规定与具体的机器数的形式有关)。
机器零: 计算机保存数字的位有限,所能表示最小的数也有范围, 其中有一个范围之中的数据无法精确表示,当实际的数据处在这个无法精确表示的数据范围时计算机就将该数作为机器零来处理,因此,计算机中的机器零其实对应的不是一个固定的数,而是一个数据表示范围。
BCD 码: 用 4 位二进制数来表示 1 位十进制数中的 0~9 这 10 个数码,即二进制表示的十进制数。
汉字内码: 计算机内部存储、处理加工和传输汉字时所用的由 0 和 1 符号组成的代码。
码距: 一组编码中对应位上数字位不同的最小个数。
奇偶校验:通过检测校验码中 1 的个数的奇 / 偶性是否改变来判断数据是否出错的一种数据校验方法。
海明校验:是一种基于多重奇校验且具有检测与纠正错误的校验方法。其基本原理是 将有效信息按某种规律分成若干组,每组安排一个校验位进行奇偶测试,就能提供多位检错信息,以指出最大可能是哪位出错,从而将其纠正。
循环冗余校验: 是数据通信领域中最常用的一种 具有检测与纠正错误能力 差错校验码, 基利用生成多项式并基于模 2 运算建立编码规则。
检错:检测被传送的信息中是否发生差错。
纠错: 纠正信息在传送或存储过程中所发生的错误。
二、练习
1) 为什么计算机中采用二进制 ?
答: 因为二进制具有运算简单和表示简单的优点,除此之外还有可靠和容易实现等特点。
具体来说,是因为:
( 1 )技术实现简单,计算机是由逻辑电路组成,逻辑电话通常只有两个状态,开关
的接通与断开,这两种状态正好可以用“ 1 ”和“ 0 ”表示。
( 2 )简化运算规则:两个二进制数和、积运算组合各有三种,运算规则简单,有利
于简化计算机内部结构,提高运算速度。
( 3 )适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好
与逻辑代数中的“真”和“假”相吻合。
( 4 )易于进行转换,二进制与十进制数易于互相转换。
2) 为什么计算机中采用补码表示带符号的整数 ?
答: 采用补码运算具有如下两个特征: ( 1 ) 因为使用补码可以将符号位和其他位统一处理,同时,减法也可以按加法来处理,即如果是补码表示的数,不管是加减法都直接用加法运算即可实现。 ( 2 ) 两个用补码表示的数相加时,如果最高位(符号位)有进位,则进位被舍弃。 这样的运算有两个好处: ( a ) 使符号位能与有效值部分一起参加运算,从而简化运算规则。从而可以简化运算器的结构,提高运算速度;(减法运算可以用加法运算表示出来。) ( b ) 加法运算比减法运算更易于实现。使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计。
3) 浮点数的表示范围和精确度分别由什么决定 ? 字长一定时浮点数的表示范围与精确度之间有和关系 ?
答:浮点数的表示范围由阶码的位数决定,精确度由尾数的位数决定。 当机器字长一定时,分给阶码的位数越多,尾数占用的位数就越少,则数的表示范围越大。而尾数占用的位数减少,必然会减少数的有效数位,即影响数的精度。
4) 汉字输入码、机内码和字型码在汉字处理过程中各有何作用?
答:汉字输入码、机内码和字型码,分别用于汉字的输入、汉字在计算机内的处理以及汉字的显示和打印。 具体来说,计算机要对汉字信息进行处理,首先要将汉字转换成计算机可以识别的二进制形式并输入到计算机,这是由汉字输入码完成的;汉字输入到计算机后,还需要转换成内码才能被计算机处理,显然,汉字内码也应该是二进制形式。如果需要显示和打印汉字,还要将汉字的内码转换成字形码。
5) 在机内码中如何区分两个 ASCII 码字符和一个汉字 ?
答:将一个汉字看成是两个扩展 ASCII 码,使表示 GB2312 汉字的两个字节的最高位都为 1 ,而每个 ASCII 码字符中每个字节的最高位为 0 。这样就能区别一个机内码到底对应一个汉字还是两个西文字符。
6) “ 8421 码 就是二进制数”。这种说法对吗?为什么?
答:这种说法是不对的。 8421 码 是一种最简单的有权码, 它选取 4 位二进制数的前 10 个代码 0000 ~ 1001 分别对应表示十进制数的 10 个数码。若按权求和,和数就等于该代码所对应的十进制数。 8421 码 是一种编码方式,用于十进位制与二进制数之间的转换。 而 二进制数是用 0 和 1 两个数码来表示的数。二者是不同的概念,不能等同。
7) 如何识别浮点数的正负?浮点数能表示的数值范围和数值的精确度取决于什么?
答:当采用一般浮点数格式表示浮点数时 , 阶码和尾数都各包含一位符号位。浮点数的正负由尾数的的符号位决定。当采用 IEEE754 格式时,通过数符就能判断出浮点数的正负。 浮点数能表示的数值范围和数值的精确度,分别取决于阶码的位数和尾数的位数。
8) 简述 CRC 的纠错原理。
答:发送部件将某信息的 CRC 码传送至接收部件,接收部件收到 CRC 码后,仍用约定的生成多项式 G(x) 去除,若余数为 0 ,表示传送正确;若余数不为 0 ,表示出错,再由余数的值来确定哪一位出错,从而加以纠正。具体的纠错原理如下: ( 1 ) 不论错误出现在哪一位 , 均要通过将出错位循环左移到最左边的一位上时被纠正; ( 2 ) 不为零余数的具有循环特性。即在余数后面补一个零除以生成多项目式 , 将得到下一个余数 , 继续在新余数基础上补零除以生成多项式 , 继续该操作,余数最后能循环到最开始的余数。 ( 3 ) CRC 就是利用不为零余数的循环特性 , 在循环计算余数的同时,将收到的 CRC 编码同步移动,当余数循环到等于最左边位出错对应的余数时,表明已将出错的位移到 CRC 码的最左边 , 对出错位进行纠错。 ( 4 ) 继续进行余数的循环计算 , 并同步移动 CRC 编码 , 当余数又回到最开始的值时 , 纠错后的 CRC 码又回到了最开始的位置。至此,完成 CRC 的纠错任务。
9)写出下列各数的原码、反码和补码。
0 , 一 0 , 0.10101 , 一 0.10101 , 0.11111 , 一 0.11111 , - 0.10000 , 0.10000 解: x=0 ,则[+ 0 ] 原 = 0.00 … 0 , [ + 0 ] 反 = 0.00 … 0 ,[+ 0 ] 补 = 0.00 … 0 ; x=-0 ,则[- 0 ] 原 = 1.00 … 0 , [ - 0] 反 = 1.11 … l , [ - 0] 补 = 0.00 … 0 ; x= 0.10101 ,则[ x ] 原 = 0.10101 , [x] 反 = 0.10101 , [x] 补 = 0.10101 ; x= 一 0.10101 ,则[ x ] 原 = 1.10101 , [x] 反 = 1.01010 , [x] 补 = 1.01011 ; x= 0.11111 ,则[ x ] 原 = 0.11111 , [x] 反 = 0.00000 , [x] 补 = 0.00001 ; x= 一 0.11111 ,则[ x ] 原 = 1.11111 , [x] 反 = 1.00000 , [x] 补 = 1.00001 ; x= - 0.10000 ,则[ x ] 原 = 1.10000 , [x] 反 = 1.01111 , [x] 补 = 1.10000 ; x= 0.10000 ,则[ x ] 原 = 0.10000 , [x] 反 = 0.10000 , [x] 补 = 0.10000 。
10)已知 x = 0.10110,y = —0.01010, 求:
[x/2] 补 , [x/4] 补 , [y/2] 补 , [2y] 补 解: [x] 原 =0.10110=[x] 反 =[x] 补 , 所以 [x/2] 补 =0.010110 , [x/4] 补 =0.0010110 ; [y] 原 =1.01010 , [y] 反 =1.10101 , [y] 补 =1.10110 , 所以 [y/2] 补 =1.110110 , [2y] 补 =1.0110 。
11)C 语言中允许无符号数和有符号整数之间的转换 , 下面是一段 C 语言代码 , 给出在 32 位计算机中上述程序段的输出结果并分析原因 。
|
|
原因: x 是 int 型,在计算机中以补码形式存在。 %u 以无符号输出, %d 输出真值 , 所以 x=4294967295=-1 。 u=2 31 是一个无符号数,无溢出,由于首位为 1 %u 符号输出第一位为非符号位,所以是 2147483648 %d 第一位为符号位,所以是负数,取反加 1 还是 2 31 所以是 -2147483648 。
12)用 IEEE754 32位浮点数标准表示十进制数
a) b) 3.1415927 c )64000 解: a) 首先分别将整数和分数部分转换成二进制数 : =-110.101 移动小数点,使其 变成 1.M 的形式: -110.101=-1.10101*2 2 于是得到: S=0, e = 2 , E= 10 + 01111111 = 10000001 , M = 10101 最后得到 32 位浮点数的二进制存储格式为: 1 100 0000 1 101 0100 0000 0000 0000 0000= ( C0D40000 ) 16 b) 首先分别将整数和分数部分转换成二进制数: 3.1415927 = 11.00100100001111110110101 移动小数点,使其 变成 1.M 的形式 11.00100100001111110110101 = 1.100100100001111110110101 × 2 于是得到: S=0, e = 1 , E= 1 + 01111111 = 10000000 , M = 10010010000111111011010 最后得到 32 位浮点数的二进制存储格式为: 0 100 0000 0 100 1001 0000 1111 1101 1010= ( 40490FDA ) 16 c) 首先将 6400 转换成二进制数: 64000 =1100100000000 移动小数点,使其 变成 1.M 的形式 1100100000000=1.100100000000 × 2 12 于是得到: S=0, e = 12 , E= 1100 + 01111111 = 10001011 , M = 1001 最后得到 32 位浮点数的二进制存储格式为: 0 100 0101 1 100 1000 0000 0000 0000 0000=( 45C 80000) 16
13)求与 IEEE754 32 位浮点数 43940000H 对应的十进制数。
解: 43940000H= ( 0 100 0011 1 001 0100 0000 0000 0000 0000 ) 2 S=0 , E= ( 10000111 ) 2 -127=8 , M=1.00101 所以表示数为 100101000 ,对应的十进制数为 296 。
14)设有效信息为 01011011,分别写出奇校验码和偶校验码。如果接收方收到的有效信息为 01011010,说明如何发现错误。
解:奇偶校验位分别为: 0 和 1 , 奇校验码: 01011011 0 偶校验码: 01011011 1 如果采用奇校验,则发送方发出的奇校验码 x= 01011011 0 (前 8 位 是 有效信息位,最后一位 是 校验位), 如果接收方收到的 x=01011010 0 ( 只有 1 位出错,最后一个 0 是校验位 ), 接收方按奇校验方式根据 01011010 计算得到的验位 C ’ = 1 ,与从信息中读到得校验码的取值不同,表明传送的信息发生了错误。 如果采用偶校验,利用相似的方法可以发现错误。
15)由6个字符的7位ASCII编码排列,再加上水平和垂直偶校验位构成如表2.23的行列结构(最后一列为水平奇偶校验位,最后一行为垂直奇偶校验位)
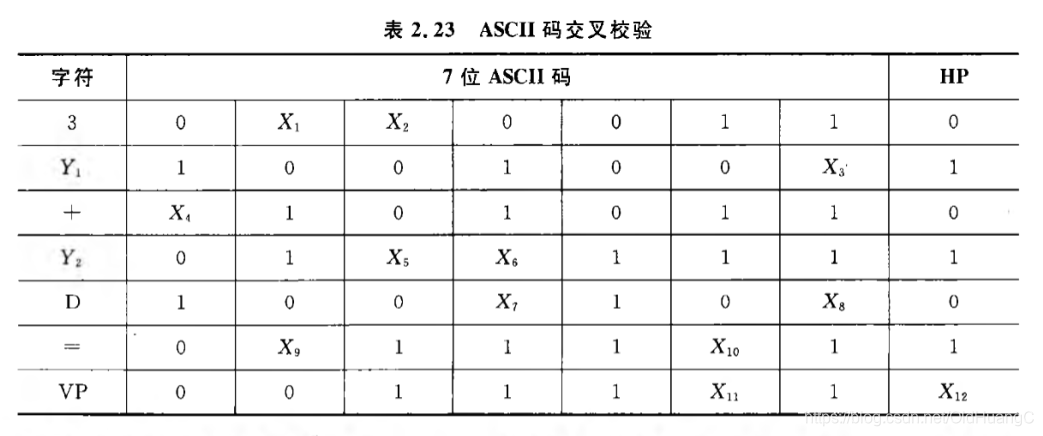
则 X 1 X 2 X 3 X 4 处的比特分别为 _1110 _ ; X 5 X 6 X 7 X 8 处的比特分别为 1000 ; X 9 X 10 X 11 X 12 处的比特分别为 _1011 _ ; Y 1 和 Y 2 处的字符分别为 I _ 和 __ 7 _ 。 解答思路:利用 交叉奇 / 偶校验 原理来确定各个 X 值,再查询 ASCII 码表获知 Y 1 和 Y 2 是什么字符。
16)设8位有效信息为01101ll0,试写出它的海明校验码。给出过程,说明分组检测方式,并给出指误字及其逻辑表达式。如果接收方收到的有效信息变成01101111,说明如何定位错误并纠正错误。
解:被检验位有 8 位,设检验位有 r 位 因为: 8+r<=2 r -1 r=4; 设四位分别为 P1,P2,P3,P4 海明码为: P1 P2 0 P3 1 1 0 P4 1110 P1 : 3 , 5 , 7 , 9 , 11 P2 : 3 , 6 , 7 , 10 , 11 P3 : 5 , 6 , 7 , 12 P4 : 9 , 10 , 11 , 12 所以 P1=1 , P2=1 P3=0 P4=1 海明码为: 110011011110 指错位 G1 : 1 , 3 , 5 , 7 , 9 , 11 G2 : 2 , 3 , 6 , 7 , 10 , 11 G3 : 4 , 5 , 6 , 7 , 12 G4 : 8 , 9 , 10 , 11 , 12 G1=0 , G2=0 , G3=0 , G4=0