2.2定点与浮点数据表示
一、定点数据表示
定点表示法约定机器中所有数据的小数点位置固定，其中，将小数点的位置固定在数据的最高数位之前(或符号位之后）的数据表示称为定点小数，而将小数点固定在最低数位之后的数据表示称为定点整数。另外，由于小数点位置固定，因而小数点可不必再用记号表示，也无需存储。
1.定点小数
设定点小数T的形式为X=X0. X1X2 …Xn，符号位X0用来表示数的正负，小数点的位置是约定的，机器中并不用器件去指示它。X1~Xn是数值的有效部分，也称为尾数，X1为最高有效位。
2 .定点整数
设定点整数X的形式为工X=X0X2X3X4~Xn. 定点数能表示的数据范围与下列因素有关。 1)字长。一般而言，字长越长，表示的数据范围就越大。 2)所采用的机器数表示方法。通过前面对几种不同机器数的分析可知，补码和移码数据表示所能表示的数据范围比原码和反码所能表示的数据范围要多一个数据单位。
3.定点数的数据表示范围
定点数的数据表示范受字长及采用的机器数形式等因素有关。
二、浮点数据表示
浮点表示法是小数位置点在数据中不固定，即小数点在数中可以浮动的一种数据表示方法，它由阶码和尾数两部分组成，其中阶码的位数决定数据的范围，尾数的位数决定数据的精确度。
1 .浮点数据表示的一般格式
EsE1E2E3E4E5E6…EnMsM1M2M3M4…Mk
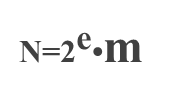Es表示阶码的符号,E1~En为阶码的值。Ms表示尾数的符号（也决定整个数的正负）M1 ~Mk构成尾数，尾数是小于1的数。其中，阶码位数决定数的范围，尾数位数决定数的精确度。 分给阶码的位数越多，则留给尾数的位数就越少，所以说如果要表示更大的范围，就必须要牺牲精确度。反之亦然。
不足之处： 数据的移植性太差，不同思系统可能根据自己的浮点数格式从中提取不同位数的阶码。
2 .IEEE浮点数据表示
在浮点数据表示中，不同机器可能选用不同基、不同的阶码及尾数的位数，从而导致不同机器浮点数据表示的差异性较大，不利于软件的移植。为此，美国电气及电子工程师协会IEEE于1985年提出了浮点数标准IEEE 754，现在该浮点数标准已被主流计算机所采用。 单精度32位浮点数格式： 符号位S+8位偏指数E+23位有效尾数M 双精度64位浮点数格式： 符号位S+8位偏指数E+23位有效尾数M
指数采用偏移值，其中单精度偏移值为127，双精度为1023，将浮点 数的阶码值变成非负整数,便于浮点数的比较和排序。 IEEE754尾数形式为1.XXXXXX,其中M部分保存的是XXXXXX(1被隐 藏)，从而可保留更多的有效位，提高数据表示的精确度
以32位单精度为例，IEEE754格式相对应的32位浮点数的真值可表示为：
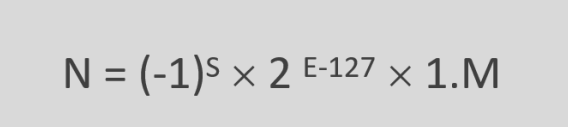对于IEEE754的E和M取值的不同，其表示的意义也不同
IEEE75432位浮点数与对应真值之间的变换流程：
