2进制8进制10进制16进制之间的转换
目录
二进制、八进制和十六进制向十进制转换
二进制、八进制和十六进制向十进制转换都非常容易，就是“按权相加”。所谓“权”，也即“位权”。
假设当前数字是 N 进制，那么：
- 对于整数部分，从右往左看，第 i 位的位权等于N^(i-1)
- 对于小数部分，恰好相反，要从左往右看，第 j 位的位权为N^-j。
将十进制转换为二进制、八进制、十六进制
将十进制转换为其它进制时比较复杂，整数部分和小数部分的算法不一样。 #### 1) 整数部分
十进制整数转换为 N 进制整数采用“除 N 取余，逆序排列”法。具体做法是：
- 将 N 作为除数，用十进制整数除以 N，可以得到一个商和余数；
- 保留余数，用商继续除以 N，又得到一个新的商和余数；
- 仍然保留余数，用商继续除以 N，还会得到一个新的商和余数；
- ……
- 如此反复进行，每次都保留余数，用商接着除以 N，直到商为 0 时为止。
把先得到的余数作为 N 进制数的低位数字，后得到的余数作为 N 进制数的高位数字，依次排列起来，就得到了 N 进制数字。
十进制数字 36926 转换成八进制的过程：
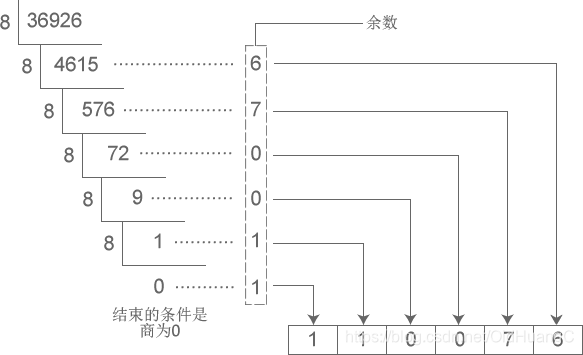
十进制数字 42 转换成二进制的过程：
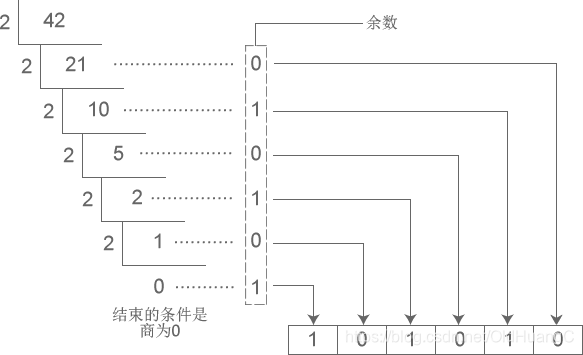
2) 小数部分
十进制小数转换成 N 进制小数采用“乘 N 取整，顺序排列”法。具体做法是：
- 用 N 乘以十进制小数，可以得到一个积，这个积包含了整数部分和小数部分；
- 将积的整数部分取出，再用 N 乘以余下的小数部分，又得到一个新的积；
- 再将积的整数部分取出，继续用 N 乘以余下的小数部分；
- ……
- 如此反复进行，每次都取出整数部分，用 N 接着乘以小数部分，直到积中的小数部分为 0，或者达到所要求的精度为止。 把取出的整数部分按顺序排列起来，先取出的整数作为 N 进制小数的高位数字，后取出的整数作为低位数字，这样就得到了 N 进制小数.
十进制小数 0.930908203125 转换成八进制小数的过程：
0.6875 转换成二进制小数的过程:
前17个十进制整数与二进制、八进制、十六进制的对应关系
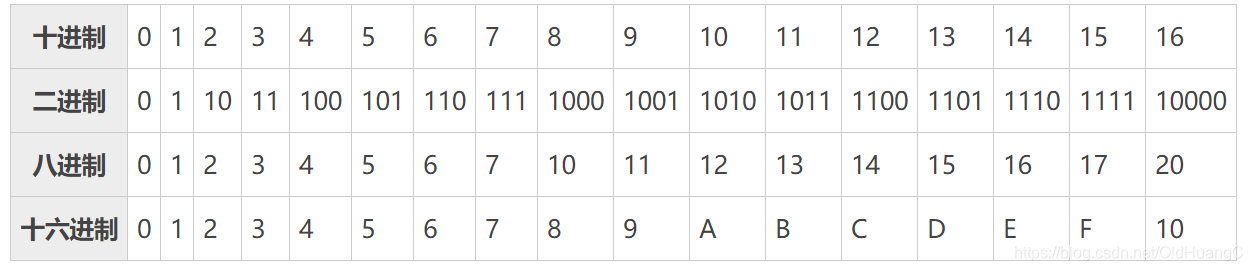
神奇的8421法
当我学完数电之后，发现进制的转化可以更加简单了。比如（1100 1011）二进制转化为八进制就是（313）8，转化为十进制就是128+64+8+2+1=（203）10，转化为十六进制就是（CB）16
原理
十进制由于不是2的整数次方得出的进制，因此需要特别注意一下。这种方法可以推广到多进制，比如32进制，就变成了16 8 4 2 1。只是日常生活中我们用8421已经足以了。
参考资料