3.1定点数运算及溢出检测
数据在计算机中是以一定的编码方式表示的，常用的编码有原码、反码、补码和移码。同一种算术运算，使用不同的编码，有不同的运算法则。由第2章对不同机器数特点的分析可知，采用补码数据表示，不仅符号位同数值位一起参加运算，而且还可以把减法变成加法实现。因此基于补码数据表示的定点补码加减法运算具有运算规则简单，易于实现等优点。
定点数的运算
定点数的运算是基于定点补码来进行运算的！
定点数的加法
定点数加法的运算满足这个公式：
[X]补 + [Y]补 = [X + Y]补
例：
理解：要求X+Y，首先将X转化为补码的形式（正数：0+原数，负数：1+余各项取反，最后在末尾+1），利用公式X[补] + Y[补] = [X + Y]补 求得[X + Y]补 ，然后再转换为原码。
再举个例子：
设 x =0 .1010，y = - 0.0100，求x + y =？
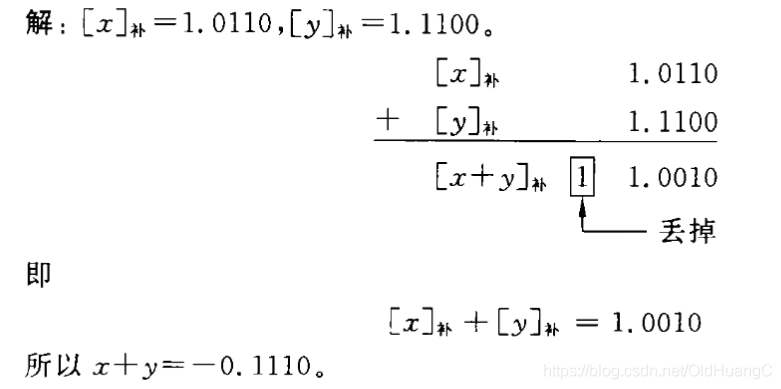
[Y]补和[-Y]补的规律
通过推到我们得出一个很重要的规律： （1）已知[Y]补快速求出[ - Y]补 从右向左扫描[Y]补，在遇到数字1及之前，直接输出遇到的数字，遇到第一个1之后，取反输出，即可得到[-Y]补。 （2）已知[Y]补快速求出[ - Y]补 从右向左扫描[ - Y]补，在遇到数字0及之前，直接输出遇到的数字，遇到第一个0之后，取反输出，即可得到[Y]补。
定点数的减法
定点数减法的运算满足这个公式：
[X + Y]补 = [X]补 - [Y]补 = [X]补 + [-Y]补
例：
再举两个个例子：设X=-0.1001，y=-0.0110 ,求 x - y
设X= 0.1001，y = 0. 0110,求[x]补一[y]补
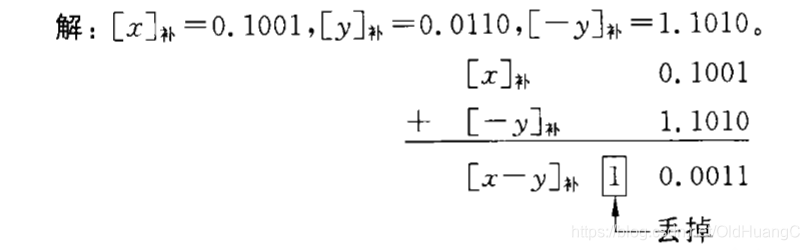
溢出
溢出的概念及其判断方法
1、运算结果超出数据类型所能表示数据范围的现象称为溢出。上面两个例子的运算结果都是错误的，其原因就是因为运算的结果超过了定点小数所能表示的数据范围，两个正数之和应该等于一个正数，两个负数之和应该等于一个负数，但上面的例子中却并非如此。
2、由于机器字长是确定的，所以能表示的数据范围也是有限的，溢出现象不可避免。而溢出往往可能导致有效数字丢失或直接导致错误的运算结果，因此，对于计算机系统设计者而言，必须解决溢出的判断问题，以便溢出发生时计算机应能做出相应的处理。
有多种方法可以检测出溢出，下面将主要介绍常见的3种方法。
1）溢出检测第一种方法
1)根据操作数和运算结果的符号位是否一致进行检测显然，只有两个符号相同的数相加时才有可能产生溢出，因此，可根据操作数和运算结果的符号位是否一致进行检测。
基于该方法实现溢出检测的逻辑表达式如公式所示：
2）溢出检测第二种方法
2)根据运算过程中最高数据位的进位与符号位的进位位是否一致进行检测设运算时最高有效数据位产生的进位信号为C1，符号位产生的进位信号为C0
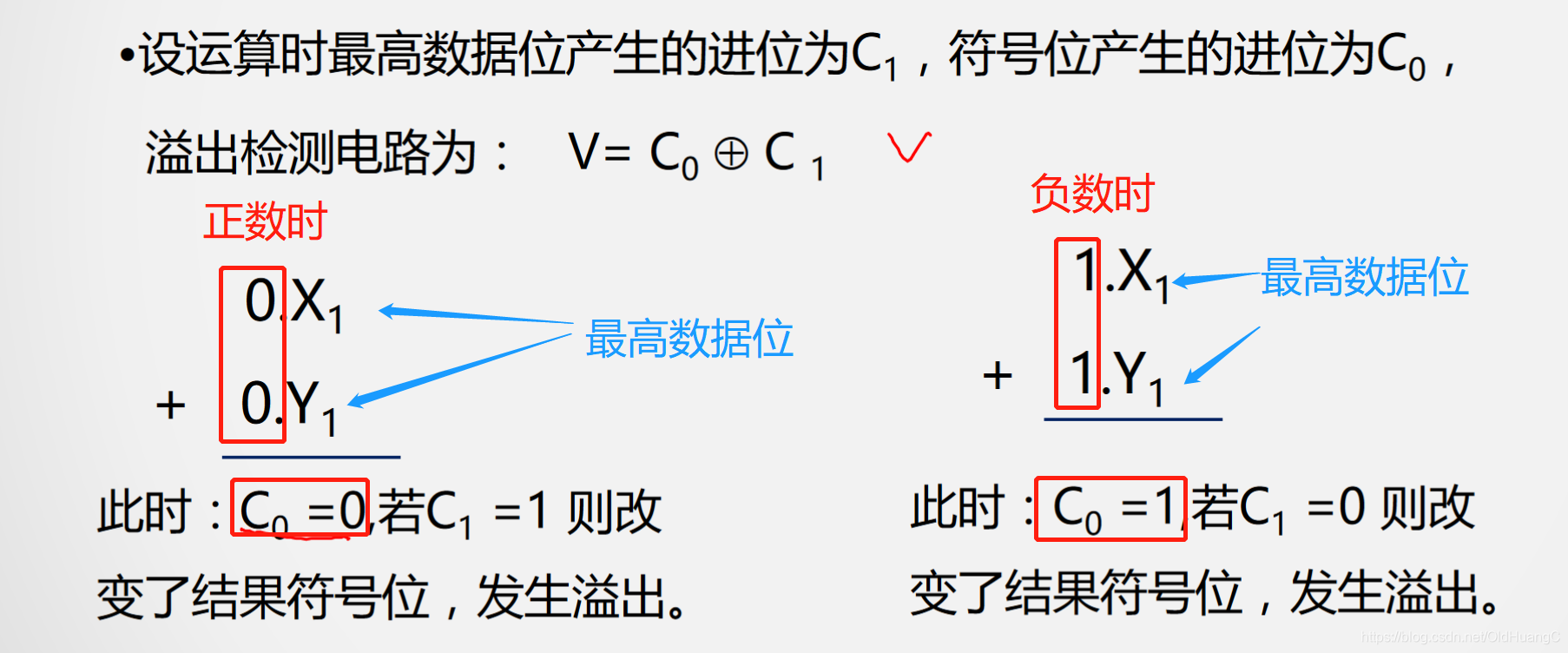
当两个正数相加时，C0必然等于0，此时判断最高数据位相加产生的进位是1还是0，如果没有产生进位（也就是0），则无溢出。若进位为1，则改变了结果的符号位，发生溢出。负数相加时同理。
3）溢出检测第三种方法
利用变形补码进行检测变形补码，即用两个二进制符号位来表示数据的符号位（例如：Xf1，Xf2，X0,X1,X2…….Xn Xf1、Xf2分别称为第一符号位和第二符号位），其余与补码相同。对定点小数而言，采用变形补码后，其模为4,因此，也称为“模4补码”；对整数而言，采用变形补码后，其模为2"+2 ( n为数值位的位数）。