3.2 定点数补码加、减运算器设计
基于上一篇文章3.1定点数运算及溢出检测的学习，这次需要完成的定点数补码加、减运算器的设计。
什么是全加器？
在开始之前，需要复习一下数字电路中学到的全加器。全加器英语名称为full-adder，是用门电路实现两个二进制数相加并求出和的组合线路，称为一位全加器。一位全加器可以处理低位进位，并输出本位加法进位。多个一位全加器进行级联可以得到多位全加器。常用二进制四位全加器74LS283。 一位全加器的真值表如下图，其中Ai为被加数，Bi为加数，相邻低位来的进位数为Ci-1，输出本位和为Si。向相邻高位进位数为Ci
| 输入 | 输入 | 输入 | 输出 | 输出 |
|---|---|---|---|---|
| Ci-1 | Ai | Bi | Si | Ci |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
一位全加器的表达式如下：
Si=Ai⊕Bi⊕Ci-1
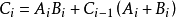
加法运算器设计
四位串行加法器的设计（基于一位全加器FA）
根据 [X]补 + [Y]补 = [X + Y]补。利用一位全加器（FA )作为基本的加法单元，低位FA的进位输出直接送入相邻高位FA的进位输人，构成一个串行进位链。
四位串行加/减法器设计
利用一位全加器（FA )作为基本的加法单元，低位FA的进位输出直接送入相邻高位FA的进位输人，构成一个串行进位链。
当P等于1时，是减法运算器。减法运算器根据 [X + Y]补 = [X]补 - [Y]补 = [X]补 + [-Y]补。如何实现【Y】补转换为【-Y】补？只需要在B输入端连接异或门，与1异或。就可以得到Bi的反码，再从C0端＋1，就可以将【Y】补转换为【-Y】补。
三种带溢出检测功能的加/减运算器
第一种
第二种
第三种
带无符号数溢出检测功能的加/减运算器
改进
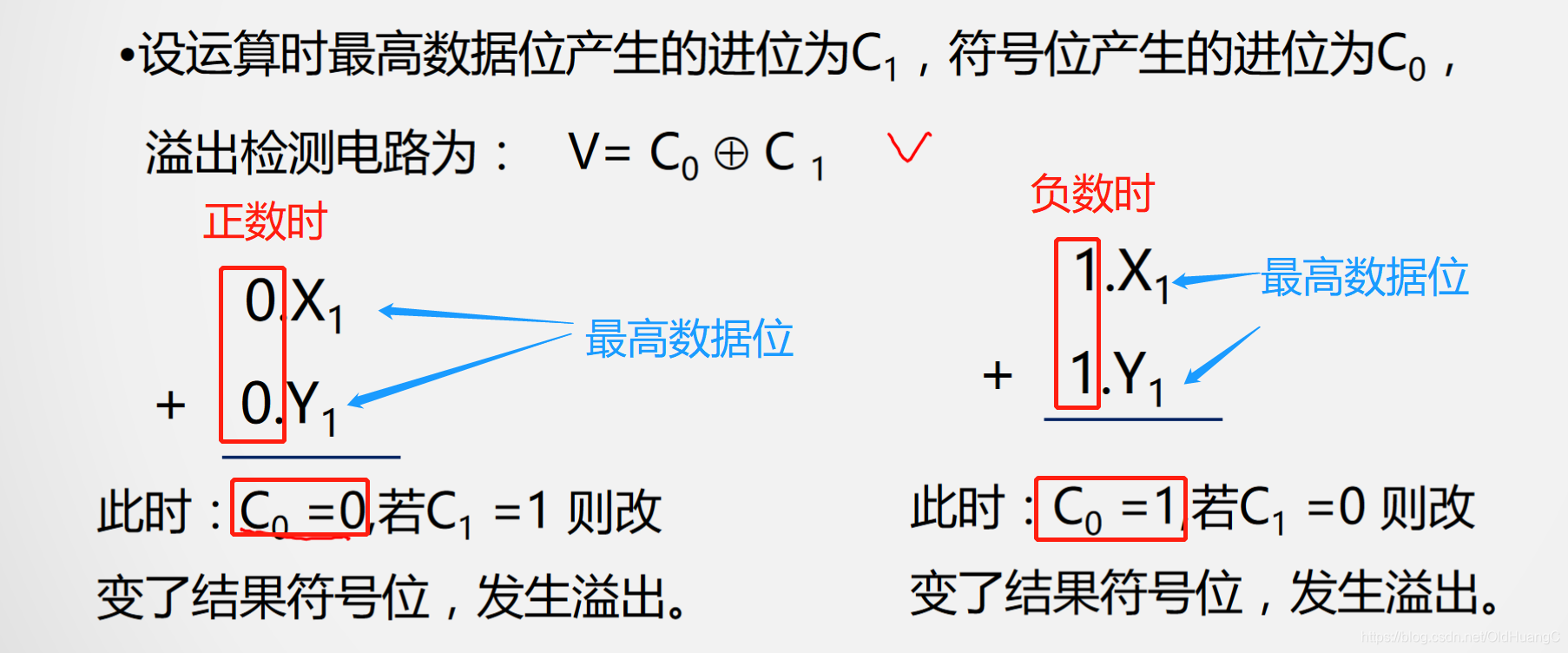
对于上面的串行加减法器，如果数据不是很大时，时延就不会明显感觉到，如果是进行大数据运算，那么串行进位的时延就很大，串行进位的运算速度慢。因此我们需要将串行改为并行，以满足大数据运算的需求。由一位全加器的表达式可知
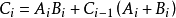
Cin都是上一位全加器的Cout，因此它需要等待上一位的Cout计算出来才能执行下一步。
但如果把Cin替换为上一位Cout的表达式，则不需要等待上一步运算。大大降低了时延。
从C4中又可以得到进位产生函数G和进位传输函数P，P相当于把C0传输到C4的输出，如果P等于1时，C0就为了C4做了贡献。
因此得到了四位并行ALU，那如何进行由四位并行ALU去构造位数更多的ALU呢？答案很简单，只要把他们像四位FA串行连接的方法即可。那就分成了四段，每段又变成了串行运算。我们需要把这16位段间串行的ALU改造成完全并行的ALU。
对每一段的进位输出和进位输入得到表达式进行分析得到，C4C8C12C16也是像刚开始的串行进位一样，因此利用代入的方法，消除串行进位和相互依存的关系，构成一个16位完成并行的ALU。注意：16位完全并行ALU也有进位产生函数G和进位传输函数P